Cue Soothing Minecraft — Relaxing Farm Morning. I'm tending the fields, watching the river flow. My brother walks by, saying hi. What's missing?

A brother-seeking missile with an explosive warhead enough to crack his cute Netherite armor, of course! This is my journey of developing such a thing with the mc_missile Minecraft mod. Follow this article and you too will have a fire-and-forget, top-attack, Infrared-homing missile at your disposal.

The Starting Point

The server we're playing on runs the mc_missile Minecraft mod. It allows all players to program guided missiles and fire them from a crossbow or dispenser.

A missile is built from components, each with a price tag and effects on the missile. For us only the rocket motor, air frame and seeker head matter.

Like the player (including my brother) the missile is an entity in Minecraft. The missile has

• a position $p = \begin{pmatrix} p_1 \\ p_2 \\ p_3 \end{pmatrix} \in \mathbb{R}^3$ (with the elevation $p_2$),

• velocity $v \in \mathbb{R}^3$,

• pitch $\theta \in [-90, 90]$ and

• yaw $\psi \in [-180, 180]$.

  These angles are in degrees and there's no roll. Additionally, they are the negated angles displayed in the Mincraft F3 Menu. That's because projectiles have flipped headings for some reason: $\theta=90$ is up, $\theta=-90$ down and $\psi \in \{-180, 180\}$ is north, $\psi = 90$ east, $\psi = 0$ south and $\psi = -90$ west.

Minecraft updates the missile's state every tick (20 times a second). The update in tick $t \in \mathbb{N}_0$ is separated into three stages:

1. Receive the control input: The missile's only input method is an unrealisticly beefy control moment gyroscope. So the player's guidance code produces a requested change in pitch $\theta_{in}$ and yaw $\psi_{in}$. It has no direct control over the missiles position, velocity, or thrust — only the rotation.

2. Update the missile's state: The gyroscope is powerful but not overly powerful. When the control input is too large (larger than $M_r$ defined by the airframe), it is scaled down linearly:

   $$\begin{aligned} l &= \sqrt{\theta_{in}^2 + \psi_{in}^2} \\ \begin{pmatrix} \theta_{in} \\ \psi_{in} \end{pmatrix} &\rightarrow \max{\left\{\frac{M_r}{l}, 1\right\}} \begin{pmatrix} \theta_{in} \\ \psi_{in} \end{pmatrix}. \end{aligned}$$

   With this, Minecraft applies the adjusted control input plus some random noise.

   $$\begin{aligned} \theta &\rightarrow \theta + \theta_{in} + N_r \\ \psi &\rightarrow \psi + \psi_{in} + N_r \\ \end{aligned}$$

   Each $N_r$ is normally distributed noise dependent on the air frame used by the missile. So you don't have perfect control over the missiles rotation, there is always some variance.

   Now the acceleration $a \in \mathbb{R}^3$ can be calculated from the rotation vector $r \in \mathbb{R}^3$, the current thrust $T(t) \in [0, \infty)$ and gravity $g = \begin{pmatrix} 0 \\ -\|g\| \\ 0 \end{pmatrix} \in \mathbb{R}^3$.

   $$\begin{aligned} r & = \begin{pmatrix} \sin(\psi) \cos(\theta) \\ \sin(\theta) \\ \cos(\psi) \cos(\theta) \end{pmatrix} \\ a & = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \\ & = \left(T(t) + N_T \right) \cdot r + g \end{aligned}$$

   $N_T$ is normally distributed noise and like the thrust function $T$ defined by the rocket motor.

   Lastly, the velocity and position are updated with the airframe defined drag $d \in [0, 1)$.

   $$\begin{aligned} v &\rightarrow (1 - d) \cdot (v + a) \\ p &\rightarrow p + v \end{aligned}$$

3. Now that the missile's state has been updated Minecraft sends that state to the player's guidance code. All these values contain some variance, too — depending on the missile's inertial measurement unit. The guidance server has a little less than 50ms to send the rotation change for the next tick.

In the first tick ($t=0$), the missile doesn't have guidance input yet and thus flies straight ahead with the velocity and rotation of the shooter. No variance is applied here.

Disclaimer: As you can see the flight dynamics of Minecraft missiles don't have anything to do with real missiles. There are no aerodynamic aspects simulated at all, for example. All we do is magically rotate a rock in vacuum. Thus the guidance code explained in this article can only be applied to the toy world that is Minecraft and nothing else. Still, it'll be fun!

So what happens when we write the simplest guidance code we can think of: doing nothing. We all like oxidized weapons so let's use Rust for this:

let mut control_input = ControlInput {
    pitch_turn: 0.0,
    yaw_turn: 0.0,
    // --snip--
};

We're probably more likely to blow ourselves up than my brother like this. (A cheaper airframe would take an even less predictable path.)

Flying a Straight Line

Let's start with compensating the rotation noise $N_r$. We can simply record the missile's heading in the first tick

self.target_pitch = missile_state.pitch;
self.target_yaw = missile_state.yaw;

and in all following ticks measure the missile's heading deviation and correct for it.

let mut control_input = ControlInput {
    pitch_turn: self.target_pitch - missile_state.pitch,
    yaw_turn: self.target_yaw - missile_state.yaw,
    // --snip--
};

Now the missile flies in a consistently straight line. It just isn't flying where we're pointing our crosshair (at my brother).

Compensating for Gravity

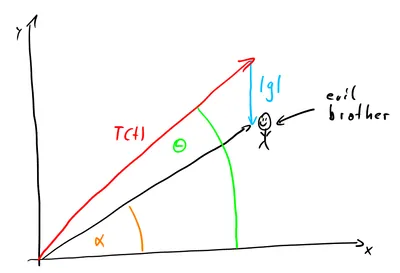
As we can see we only have to adjust our pitch: There's no gravity messing with our yaw. Given the pitch $\alpha \in [-90, 90]$ of a desired acceleration (towards my brother) what pitch $\theta$ should the rocket point in?

Assume, without loss of generality, $\psi = 90$ and ignore thrust variance. Also, assume $T(t) > \|g\|$ (otherwise we'd have to calculate a parabola when our initial velocity suffices). Then $a_3 = 0$ and we can write:

$$\begin{aligned} \tilde{a} &= \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \\ &= \|g\| \cdot \begin{pmatrix} 0 \\ -1 \end{pmatrix} + T(t) \cdot \begin{pmatrix} \cos(\theta) \\ \sin(\theta) \end{pmatrix} \end{aligned}$$

and with some trigonometry:

$$\begin{aligned} \tan(\alpha) &= \frac{a_2}{a_1} \\ &= \frac{T(t) \cdot \sin(\theta) - \|g\|}{T(t) \cdot \cos(\theta)}. \end{aligned}$$

There's no closed-form solution for $\theta$. The best we can do is rewrite it like this and use a numerical root-finding approach like Newton's method:

$$\frac{\|g\|}{T(t)} + \cos(\theta) \tan(\alpha) - \sin(\theta) = 0.$$

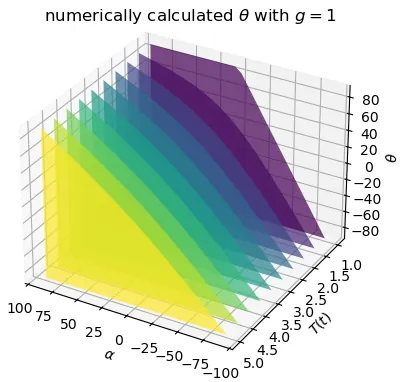
How do we do that with Rust? We use Python, calculate a lookup-table resolving $\left(\frac{\|g\|}{T(t)}, \alpha\right) \mapsto \theta$ and use that in Rust.

import numpy as np
from scipy import optimize

def f(x, thrust, target_pitch_rad, g):
    return ((g/thrust) + np.tan(target_pitch_rad)*np.cos(x) - np.sin(x))

def fprime(x, thrust, target_pitch_rad, g):
    return (-np.tan(target_pitch_rad)*np.sin(x) - np.cos(x))

# Set the gravity to 1 so that we can easily scale the effective thrust in rust.
# effective_thrust = thrust/g
g = 1
thrusts = np.linspace(1, 5, 30)
target_pitches_deg = np.linspace(-90, 90, 30)
target_pitches_rad = np.deg2rad(target_pitches_deg)
thrusts_grid, target_pitches_rad_grid = np.meshgrid(thrusts, target_pitches_rad)
target_pitches_deg_grid = np.rad2deg(target_pitches_rad_grid)

heading_pitches_rad = optimize.newton(
    f,
    target_pitches_rad_grid,
    fprime=fprime,
    args=(thrusts_grid, target_pitches_rad_grid, g)
)
heading_pitches_deg = np.rad2deg(heading_pitches_rad)

As you can see in the colourful plot, when the missile has high thrust we don't really have to correct for gravity at all and our yellow line is basically straight. When the thrust is almost as strong as the gravity, we have to adjust our heading a lot more aggressively.

Pretty nice!

IrSeeker and Top Attack

One problem with the above design is that errors along the way are added up and make the missile miss sometimes. We can fix this with the IrSeekerM missile component, which provides my brother's position every tick (when there's a line-of-sight). Then the missile can update it's target heading and fix it's past inaccuracies.

With the missile's position $p$ and some target coordinates $k$ you can calculate the desired pitch $\alpha$ and yaw $\psi$ with the below trigonometry.

pub async fn calc_alpha_psi(target_direction: Vec3) -> (f64, f64) {
    // projected onto the horizontal plane
    let vec_horizontal = Vec3::new(target_direction.x, 0.0, target_direction.z);
    let mut alpha = vec_horizontal
        .normalize()
        .dot(&target_direction.normalize())
        .acos()
        .to_degrees();
    if target_direction.y < 0.0 {
        alpha *= -1.0;
    }
    let psi = target_direction.x.atan2(target_direction.z).to_degrees();
    (alpha, psi)
}

And then the gravity corrected pitch $\theta$, $\theta_{in}$ and $\psi_{in}$ to make the missile accelerate towards the target.

I had some fun with this and implemented top-attacks, where the missile rises into the air before striking the ground at high speed. At some point the missile switches from flying to some block in the sky to flying towards my brother.

Oh, no, our missile isn't hitting any more! Why is that?

Velocity-Awareness

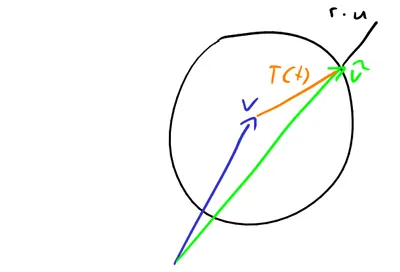
The issue is that accelerating towards my brother isn't actually what we want: We want to align our velocity $v$ so that it moves us closer towards the target. Our previous calculation simply points our acceleration vector towards the target. When $\|v\| = 0$ or $v$ is already pointing in the right direction that is correct. But at the apogee of a top-attack our missile's velocity is pointing towards the sky, not the target; so we miss.

Say our target is at $y \in \mathbb{R}^3$ and we are at $p$. Then we're asking for our new velocity $\tilde{v} = v + a$ to fulfil

$$\begin{aligned} \tilde{v} &= r \cdot u \\ \end{aligned}$$

with $r \in (0, \infty)$ and $u = y - p$.

Because of gravity the exact length of $a$ is unfortunately not known at this point. A good approximation is to ignore gravity for now and use

$$\|a\| \approx T(t).$$

You might already notice that $r \cdot u$ defines a line in direction $u$ (from the missile towards my brother) and $v + a$ a sphere around $v$ with radius $T(t)$. So we're asking for a line-sphere intersection. You could either do the math yourself or use Wikipedia and come up with

$$\begin{aligned} r_{rad} &=&& (2u^Tv)^2 - \\ & && 4\|u\|^2 \left(\|v\|^2 - T(t)^2\right) \\ r_{1,2} &=&& \frac{2u^Tv \pm \sqrt{r_{rad}}} {2\|u\|^2}. \end{aligned}$$

I use the larger $r_{1,2}$ because then we're also accelerating towards the target while keeping our velocity correctly pointed. (You could also use the smaller one and accelerate away from the target in case you want to break.) With this I know where to accelerate:

$$\frac{a}{\|a\|} = \frac{r \cdot u - v}{\|r \cdot u - v\|}.$$

We again need to compensate for gravity to calculate the right missile rotation.

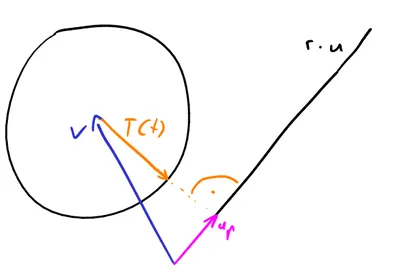
One last problem: When the above radical $r_{rad}$ is negative we can't calculate the square-root. This is the case when the sphere and line don't intersect at all. For us that means our current velocity is so far off and our thrust so weak there's no way we could reach the requested velocity this tick. In this case the best we can do is take the point of our circle closest to our line. That's equivalent to projecting $v$ orthographically onto $u$:

$$\begin{aligned} u_p &= \frac{v^Tu}{\|u\|^2} \cdot u \\ \frac{a}{\|a\|} &= \frac{u_p - v}{\|u_p - v\|} \end{aligned}$$

Again we need to compensate for gravity just like before. Doing this for a few ticks should hopefully be enough to at some point have a positive radical and use the line-sphere intersection then. Fun fact: In this situation we aren't accelerating towards the target at all. We're completely focused on getting us on course, first.

Now our top attack works all the time. (Minus that one time the proximity fuse triggered too early, whoops.)

And direct attacks work, too.

Even aerial brothers can be engaged! This only works with this design because the rocket motor is so crazily powerful. It costs something like five diamonds per rocket alone! Anything cheaper wouldn't work like this.

Other Ideas

There's a lot you could improve upon. A few of my ideas:

1. Use a different war head, the mc_missile mod offers many options.
2. Implement a boost phase where the missile clears the trees and buildings the shooter stands under before rising into the sky.
3. Guess the target's position based on the current direction (works without top-attack). Then you can save on the expensive seeker.
4. Do some parabola calculation and use a cheaper rocket motor that only has a short burn duration in the beginning.
5. Implement Proportional navigation to shoot down moving and aerial targets.
6. Use lock-on after launch to fire at targets without visual contact.
7. Generally use cheaper components and deal with the implications.
8. much, much more...

I encourage you to give the mc_missile Minecraft mod a go — it's real fun!

PS

Psst, my entire guidance code is open-source; just don't tell my brother.

PPS

My brother is actually really cool. Thanks for testing my missiles!